做了一点dp后的总结

算法日志-1

这几天间间断断地在Leetcode上面写了一二十道DP，主要是：

爬楼梯
打家劫舍
网格图

虽然说没做太多，但是也算是有了一点感觉（其实还是菜，做不出来）

---

爬楼梯

对于爬楼梯问题其实没什么好讲的，本质上和DFS很像，只不过一个是递，一个是归，这种情况下基本就是DP/DFS+记忆化搜索。

---

打家劫舍

打家劫舍分为两类，一种是下标相邻有关，一种是值域相邻有关，下标类的相对好写，只需要找出单方向的递推简化过程，转化为状态转移方程，一步步求解就好。而值域相邻有关可以使用collections.Counter生成包含 元素->次数 的字典，将最大值+1作为len(dp)，同时初始化dp[i]为 元素大小*次数，转化为下标相邻有关问题.

删除并获得点数

---

给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
Example:
输入：nums = [3,4,2]
输出：6
解释：
删除 4 获得 4 个点数，因此 3 也被删除。
之后，删除 2 获得 2 个点数。总共获得 6 个点数。

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 104

题解:

class Solution:
    def deleteAndEarn(self, nums: List[int]) -> int:
        cnt=Counter(nums)
        max_val=max(cnt.keys())
        dp=[0] * (max_val+1)
        for i , j  in cnt.items():
            dp[i] = i * j
        for i in range(1 , max_val+1):
            dp[i]=max(dp[i-1] , (dp[i-2] if i>=2 else 0) + dp[i])
        return dp[-1]

---

网格图

然后是网格图DP，网格图DP其实是抽象二维DP的铺垫(背包，最长公共子序列），这里以Leetcode 1289.下降路径最小和II为

下降路径最小和 II

---

给你一个 n x n 整数矩阵 grid ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 grid 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

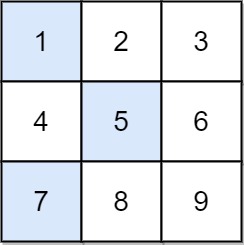
输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

输入：grid = [[7]]
输出：7

提示：

• n == grid.length == grid[i].length
• 1 <= n <= 200
• -99 <= grid[i][j] <= 99

这题最直观的想法就是找每一行的最小值，然后一路加到底，但是题目要求是非零偏移下降路径，因此要分为两种情况：

1. 与上一行最小值对齐，即 cur_index=pre_row.index(min)此时不能取最小值，只能寻求上一行的次小值（第二小的值）。
2. 不与上一行最小值对齐，cur_index!=pre_row.index(min)直接取最小值。

因此对于每一行，需要找出最小的两个值，对于需要找出可迭代对象多个最小值/最大值的场景，考虑使用heapq模块里的nsmallest / nlargest(n,iterable)
接下来只需要迭代每一行的时候，选择+=哪一个最小值就行。

代码：

class Solution:
    def minFallingPathSum(self, grid: List[List[int]]) -> int:
        for pre_row,cur_row in pairwise(grid):
            min_two=nsmallest(2,pre_row)
            for i,pre in enumerate(pre_row):
                cur_row[i]+=min_two[0] if pre!=min_two[0] else min_two[1]
        return min(grid[-1])

其中pairwise用来挨个迭代相邻的两个元素，也即：(row[0],row[1]),(row[1],row[2])…

总结下来，DP的思想很像DFS，编写的前提都是我假设前面的已经取到了所需要的值，首先要分析题目属于DP问题当中的哪一种题型，如果不够直接则思考如何转换，然后找出状态转移方程，处理边界条件(使用哨兵)，最后处理数组得到答案。

感想

归纳题型真的很重要，这个和高中数学有相似之处，Dalao做题都是一眼丁真，简单处理之后直接套框架，前期练习需要的就是对题型，框架的理解和把握程度。